src.factorize_graph_matching.construct_sparse_aff_mat

src.factorize_graph_matching.construct_sparse_aff_mat(Ke: torch.Tensor, Kp: torch.Tensor, row_idx: torch.Tensor, col_idx: torch.Tensor)

Construct sparse affinity matrix with edge-wise affinity matrix \(\mathbf{K}_e\), node-wise matrix \(\mathbf{K}_p\) and graph connectivity matrices \(\mathbf{G}_1, \mathbf{H}_1, \mathbf{G}_2, \mathbf{H}_2\)

\[\mathbf{K}=\mathrm{diag}(\mathrm{vec}(\mathbf{K}_p)) + (\mathbf{G}_2 \otimes_{\mathcal{K}} \mathbf{G}_1) \mathrm{diag}(\mathrm{vec}(\mathbf{K}_e)) (\mathbf{H}_2 \otimes_{\mathcal{K}} \mathbf{H}_1)^\top\]

where \(\mathrm{diag}(\cdot)\) means building a diagonal matrix based on the given vector, and \(\mathrm{vec}(\cdot)\) means column-wise vectorization. \(\otimes_{\mathcal{K}}\) denotes Kronecker product.

This function does not supports batched operations. This formulation is developed by “F. Zhou and F. Torre. Factorized Graph Matching. TPAMI 2015.”

Parameters

• Ke – \((1\times n_e)\) non-zero elements in edge-wise affinity matrix Ke. \(n_e\): number of non-zero elements in dense Ke

• Kp – \((1\times n_1 n_2)\) non-zero elements in node-wise affinity matrix Kp. \(n_1\): number of nodes in graph 1, \(n_2\): number of nodes in graph 2

• row_idx – \((1\times n_e)\) row indices of the non-zero elements in edge-wise affinity matrix Ke

• col_idx – \((1\times n_e)\) column indices of the non-zero elements in edge-wise affinity matrix Ke

Returns

none-zero values in the affinity matrix \(\mathbf K\), and their row/column indices (value, row-idx, col-idx)

For a graph matching problem with 5 nodes and 4 nodes, the connection of \(\mathbf K\) and \(\mathbf{K}_p, \mathbf{K}_e\) is illustrated as

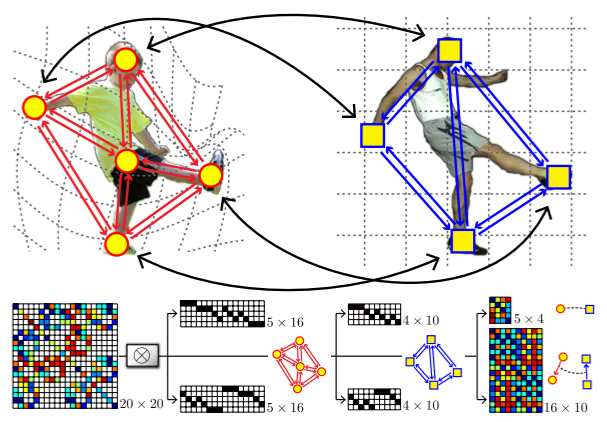
where \(\mathbf K (20 \times 20)\) is the complete affinity matrix, \(\mathbf{K}_p (5 \times 4)\) is the node-wise affinity matrix, \(\mathbf{K}_e(16 \times 10)\) is the edge-wise affinity matrix.